논문 리뷰

QIHOO-T2X: AN EFFICIENCY-FOCUSED DIFFUSION TRANSFORMER VIA PROXY TOKENS FOR TEXT-TO-ANY-TASK

3. Method

3.1 Redundancy Analysis

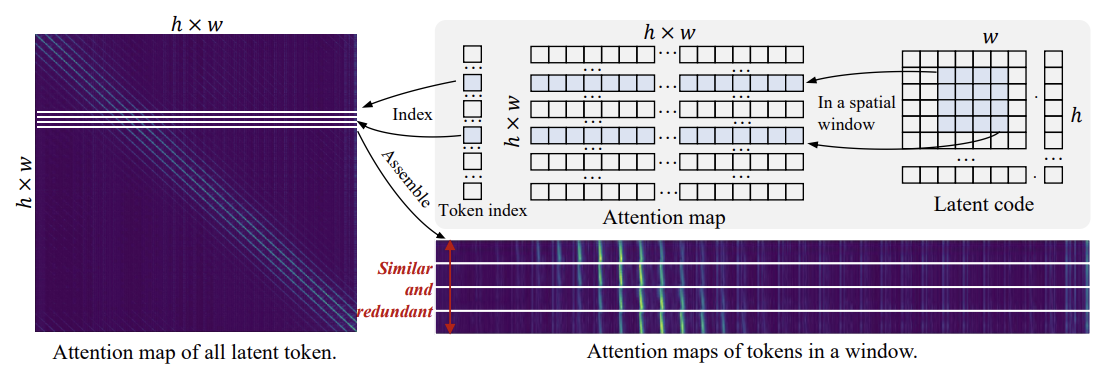
Figure 2

위 그림은 Pixart-$\alpha$ 512 resolution의 어텐션 맵이다. 그 중 같은 $4 \times 4$ 윈도우에 속하는 토큰들은 어텐션 맵이 거의 동일한 것을 볼 수 있다. 또한, 공간적으로 가까운 토큰들끼리는 유사도가 다양하지만, 멀어질수록 유사도가 일정해지는 것을 볼 수 있다.

이러한 Visual Information의 Sparsity와 Redundancy 때문에 Global Attention 매커니즘을 최적화할 필요가 있다. 이 논문에서는 Sparse Attention 전략을 적용해서 각 윈도우마다 추출한 몇 개의 Proxy Tokens끼리 Self-attention을 적용하여 연산의 복잡도를 줄인다.

3.2 Architecture of PT-DiT

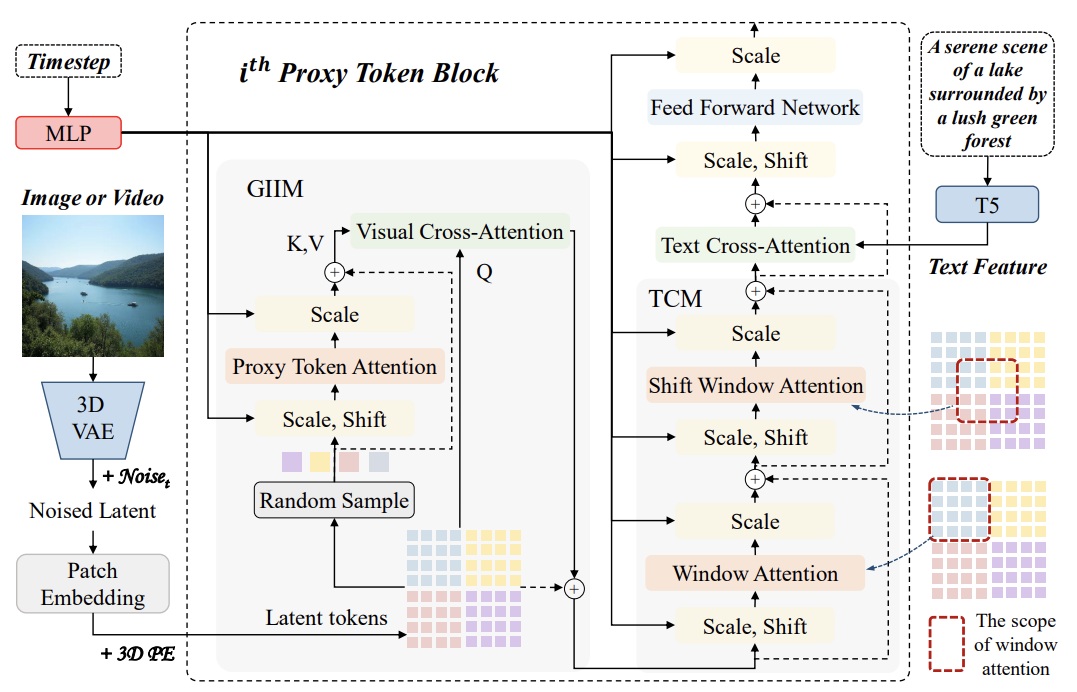
Figure 3

Latent code $z \in \mathbb{R}^{C \times F \times H \times W}$가 들어오면 path embedding을 거쳐서 latent code sequence $z_s \in \mathbb{R}^{N \times D}$가 된다. 이후 Positional Encoding을 거쳐서 Proxy Token 블록으로 들어가면 Global Information Interaction Module (GIIM)과 Texture Complement Module (TCM) 등을 거치게 된다. GIIM은 sparse하게 글로벌한 Interaction을 조사하고, TCM은 Window Attention이나 Shift-Window Attention을 통해 로컬 디테일을 조사한다.

GIIM Module

Latent code sequence $z_s \in \mathbb{R}^{N \times D}$를 \(z_s \in \mathbb{R}^{f \times h \times w \times D}\)로 reshape 한다. f는 프레임, h는 height, w는 width가 된다. 이미지의 경우 $f=1$ 이다.

프록시 토큰은 각 윈도우에서 랜덤하게 샘플된다.

\[P_a \in \mathbb{R}^{D \times \frac{f}{p_t} \times \frac{h}{p_h} \times \frac{w}{p_w}}\]

따라서 각 토큰은 $p_t \times p_h \times p_w$개의 토큰을 대표하게 된다. 이 프록시 토큰들로 Self-attention을 진행한다. 이후, cross-attention을 통해 글로벌한 비주얼 정보들을 모든 latent token들로 전달하게 된다. 모든 토큰 $z_s$가 Query가 되고, 프록시 토큰 $P_a$가 Key와 Value가 된다. 이를 식으로 나타내면 다음과 같다.

\[z_s = CS(z_s, SA(RandomSample(z_s)))\]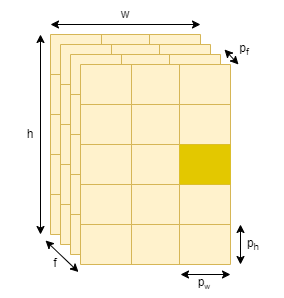

DrawIO

이런 느낌인 것 같다. 결국 $(p_f, p_w, p_h)$ 중 하나의 토큰만 살아남는 것이다. 각 토큰은 $1 \times D$ 벡터이다.

TCM Module

Sparse Proxy Token으로 인해 디테일을 표현하는 능력이 떨어지기 때문에 Localized Window Attention을 진행한다. 구체적으로 윈도우 내에서 Self-Attention을 진행하고, Grid의 영향을 줄이기 위해 Shift-Window Attention을 진행한다.

\[\hat z_s = WSA(z_s) + z_s\] \[z_w = SWSA(z_s) + \hat z_s\]

Compression Ratios

다른 해상도에 대해 윈도우 개수를 일정하게 유지해야 저해상도에서 고해상도로 훈련시킬 때 일관성을 보장할 수 있다. 동시에 윈도우의 개수를 적절하게 설정해줘야 한다.

그래서 이미지에 대해서는 해상도 256, 512, 1024, 2048에 대해 각각 Compression Ratio인 $(p_f, p_w, p_h)$를 (1, 2, 2), (1, 4, 4), (1, 8, 8), (1, 16, 16)으로 세팅한다. 비디오의 경우 $p_f = 4$ 이다.

3.3 Complexity Analysis

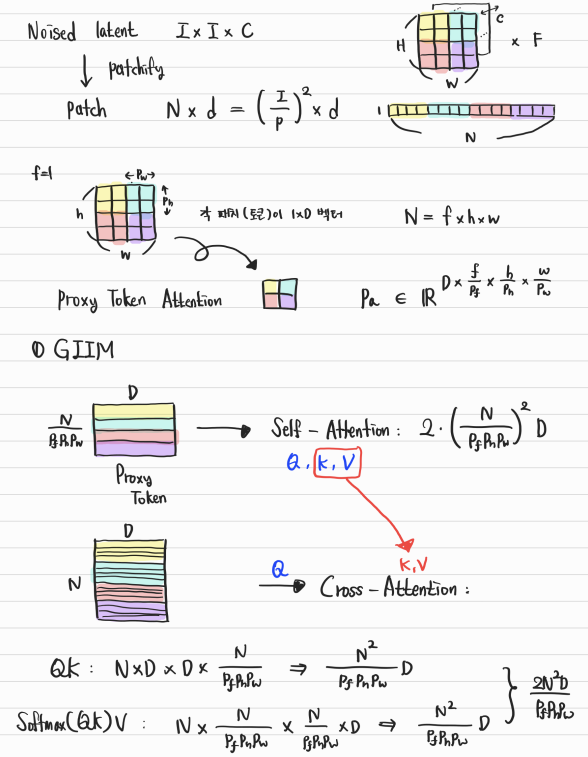
draw1

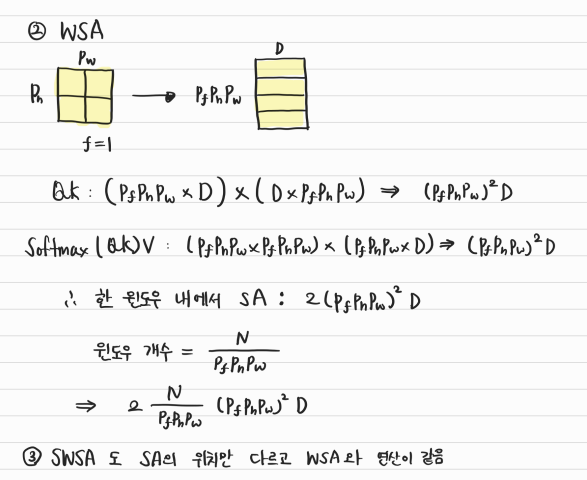
draw2

  • Self-attention의 Complexity: $QK$가 $N^2 D$, Softmax(QK)V가 $N^2 D$를 차지한다.
\[complexity = N^2 D + N^2 D + o(N^2)\]
  • GIIM과 TCM의 Complexity: $P_a \in \mathbb{R}^{D \times \frac{f}{p_t} \times \frac{h}{p_h} \times \frac{w}{p_w}}$ 에서 $f \times h \times w = N$ 인 점을 이용하면 아래 식을 금방 이해할 수 있다. 첫번째 항은 GIIM의 SA에 해당하고, 두번째 항은 GIIM의 CS에 해당한다. 마지막 항은 TCM의 WSA와 SWSA에 해당한다.
\[complexity = 2 \frac{N^2}{(p_f p_h p_w)^2} D + 2 \frac{N^2}{p_f p_h p_w} D + 4 \frac{N}{p_f p_h p_w}(p_f p_h p_w)^2 D\] \[= 2(\frac{1}{(p_f p_h p_w)^2} + \frac{1}{p_f p_h p_w} + \frac{2 p_f p_h p_w}{N}) N^2 D\]

Compression ratio $(p_f, p_h, p_w)$가 커질수록 Complexity에 이득이 많아지는 것을 확인할 수 있다. $(p_f, p_h, p_w) = (1, 2, 2), (1, 4, 4), (1, 8, 8), (1, 16, 16)$ 이면 총 Self-attention의 34.3%, 9.7%, 4.7%, 2.3% 만 차지하게 된다.

4. Algorithmic Efficiency Comparison

5

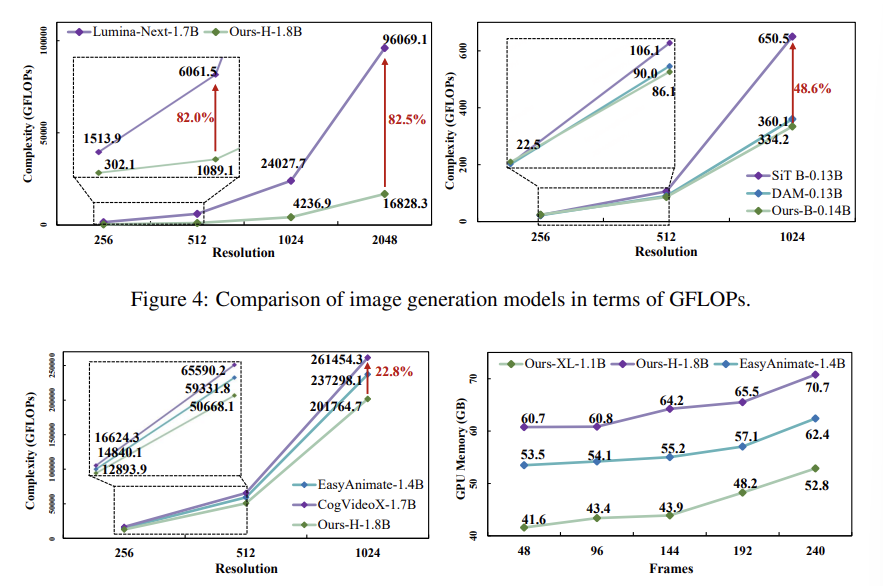
Figure 4는 이미지에서의 Complexity를 비교한 것이다. 왼쪽 그래프에서 파라미터 수가 1.8B 일 때 80% 이상 계산량이 감소하였고, 오른쪽 그래프처럼 소규모 파라미터에서도 48% 정도 계산량이 감소한 것을 볼 수 있다.

Figure 5는 비디오 생성에서 Complexity와 GPU 사용량을 비교한 것이다. 계산량도 적고 메모리 효율도 좋은 것을 볼 수 있다. 특히 EasyAnimate가 1D 어텐션만 사용하는 것과 달리 PT-DiT는 3D 어텐션을 사용함에도 계산량이 오히려 적다.

5. Conclusion

PT-DiT와 Qihoo-T2X 시리즈는 디퓨전 트랜스포머의 성능을 크게 개선하면서도 효율성을 유지할 수 있는 가능성을 보여주었다.

이 논문 좀 오타가 많은듯;
3.2.1 p_f -> p_t
3.2.3 $(p_f, p_w, p_h)$

2024/09/12