Kalman Filter
칼만 필터 원리 및 구현
칼만 필터는 루돌프 칼만이 개발한 제어 알고리즘으로, 노이즈가 포함된 관측값을 바탕으로 선형 시스템의 상태를 추정하는 재귀 필터이다.
칼만 필터의 컨셉만 읽고 싶은 분들은 I, II는 건너뛰어도 좋다.
I. Bayes’ Filter
Markov Property
\[p(x_{t+1} \vert x_{0:t}) = p(x_{t+1} \vert x_t)\]즉, 해당 시점에서 미래를 예측하는데 필요한 정보들만 갖고 있으면 완전한 상태가 된다. 과거의 정보나 독립적인 정보들은 필요하지 않다.
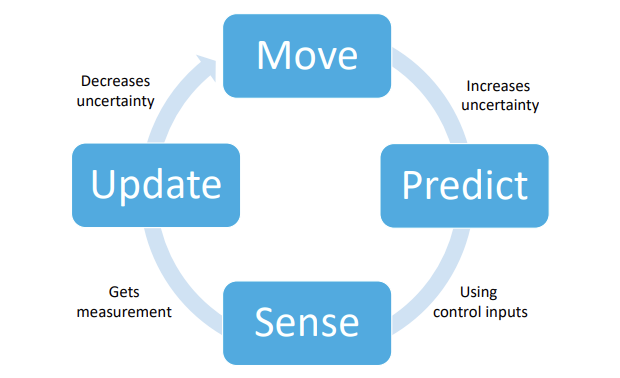
제어 시스템은 Move, Predict, Sense, Update의 반복이라고 볼 수 있다. 물체가 움직이면 불확실성이 커지고, 현재 상태와 이전 관측값을 토대로 다음 상태를 예측한다. 센서를 이용해서 관측값을 얻으면 불확실성을 없애는 방향으로 업데이트를 진행한다.
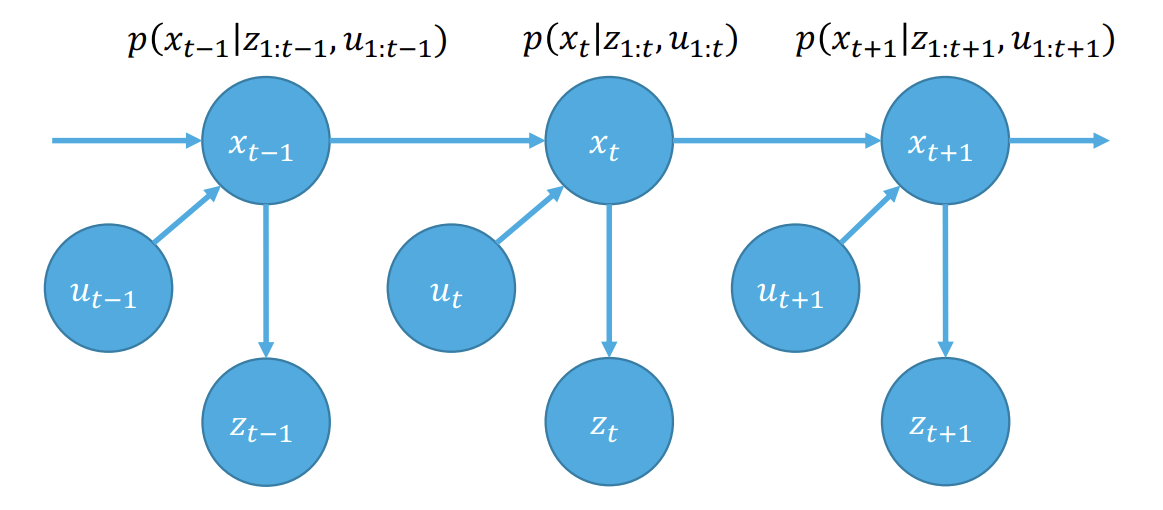
위 그림에서 Markov Assumtion을 적용하면 모델을 간단하게 나타낼 수 있다. $x_t$는 현재 상태, $u_t$는 제어 입력, $z_t$는 관측 값을 나타낸다.
Prior
초기 상태에 대한 사전 확률 분포를 나타낸다. 즉, 로봇이 처음 시작한 위치를 특정 범위 내 위치에 존재할 확률로 나타낸다.
\[p(x_0)\]Process model
시간 t에서의 상태 $x_t$가 이전 상태 $x_{t-1}$과 제어 입력 $u_t$에 의해 결정된다는 것을 나타낸다. 로봇이 이전 위치에서 얼마나 움직였는지에 따라 새로운 위치를 추정하는 것이다. 하지만 그 움직임에는 불확실성이 포함될 수 있기 때문에 확률로 표현한다.
\[p(x_t \vert x_{t-1}, u_t)\]Measurement model
시간 t에서의 측정값 $z_t$는 현재 상태 $x_t$에 의해 결정된다. 센서에 노이즈가 포함되기 때문에 확률로 표현한다. 로봇이 카메라를 이용해 자신의 위치를 측정하면, 현재 상태에서 측정된 데이터와 실제 상태의 관계를 설명하는 것이다.
\[p(z_t \vert x_t)\]Prediction Step
Process Model과 이전 상태 Prior의 곱을 이전 상태에 대해 Marginalize 한 것이다.
\[p(x_t \vert z_{1:t-1}, u_{1:t}) = \int p(x_t, x_{t-1} \vert z_{1:t-1}, u_{1:t}) \, dx_{t-1}\] \[= \int p(x_t \vert x_{t-1}, z_{1:t-1}, u_{1:t}) p(x_{t-1} \vert z_{1:t-1}, u_{1:t}) \, dx_{t-1}\] \[= \int p(x_t \vert x_{t-1}, u_t) p(x_{t-1} \vert z_{1:t-1}, u_{1:t}) dx_{t-1}\]Update Step
현재 상태의 Prior에 Measurement Model을 곱하고 Marginal Distribution으로 나눈 것이다.
\[p(x_t \vert z_{1:t}, u_{1:t}) = \frac{p(z_t \vert x_t, z_{1:t-1}, u_{1:t}) p(x_t \vert z_{1:t-1}, u_{1:t})}{p(z_t \vert z_{1:t-1}, u_{1:t})}\] \[= \eta p(z_t \vert x_t) p(x_t \vert z_{1:t-1}, u_{1:t})\]$\eta$ 는 Marginal Distribution 이다.
\[p(x \vert w, v) = \frac{p(w \vert x, v) p(x \vert v)}{p(w \vert v)}\]라는 점이 사용되었다.
정리

II. Gaussian Random Variables
Multivariate Normal Distribution
Fact 1: Jointly Normal Random Vectors
$x$가 multivariate gaussian random variable이면 \(x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\) 에서 $x_1, x_2$도 모두 gaussian random variable 이다. $x_1, x_2$를 jointly gaussian 이라고 한다.
Fact 2: Sum of Independent Gaussians
$x, y$가 독립 가우시안 분포이면 $z=x+y$ 역시 가우시안 분포이며 $\mu_z = \mu_x+\mu_y$이고 $\Sigma_z=\Sigma_x+\Sigma_y$이다.
Fact 3: Affine Transformations
$x \sim N(\mu_x, \Sigma_x)$, $y=Ax+b$ 이면 $y \sim N(\mu_y, \Sigma_y)$이고, $\mu_y = A \mu_x + b$, $\Sigma_y = A \Sigma_x A^T$ 이다.
Fact 4: Conditional Distributions
\[\mu_{x_1 \vert x_2} = \mu_1 + \Sigma_{12} \Sigma_{22}^{-1} (x_2 - \mu_2)\] \[\Sigma_{x_1 \vert x_2} = \Sigma_{11} - \Sigma_{12} \Sigma_{22}^{-1} \Sigma_{21}\]III. Kalman Filter
Assumptions
- Prior는 가우시안 분포를 따른다.
- Process model $p(x_t \vert x_{t-1}, u_t)$는 노이즈가 첨가된 선형 가우시안 분포를 따른다.
- Measurement model $p(z_t \vert x_t)$은 노이즈가 첨가된 선형 가우시안 분포를 따른다.
Prediction
\[x_t = A_t x_{t-1} + B_t u_t + n_t, n_t \sim N(0, Q_t)\] \[\hat{\mu}_t = A \mu_{t-1} + B u_t\] \[\hat{\Sigma}_t = A \Sigma_{t-1} A^T + Q\]Update
\[z_t = C_t \bar{x}_t + v_t, \quad v_t \sim N(0, R_t)\] \[x_t = \bar{x}_t\] \[\begin{bmatrix} x_t \\ z_t \end{bmatrix} = \begin{bmatrix} I & 0 \\ C & I \end{bmatrix} \begin{bmatrix} \bar{x}_t \\ v_t \end{bmatrix}\]이는 Jointly Gaussian Distribution 이므로,
\[\mu = \begin{bmatrix} \hat{\mu}_t \\ C \hat{\mu}_t \end{bmatrix}\] \[\Sigma = \begin{bmatrix} I & 0 \\ C & I \end{bmatrix} \begin{bmatrix} \hat{\Sigma}_t & 0 \\ 0 & R \end{bmatrix} \begin{bmatrix} I & C^T \\ 0 & I \end{bmatrix} = \begin{bmatrix} \hat{\Sigma}_t & \hat{\Sigma}_t C^T \\ C \hat{\Sigma}_t & C \hat{\Sigma}_t C^T + R \end{bmatrix}\]$z_t$가 관측되고 나면 $\mu_{t}$는 $\mu_{x_t \vert z_t}$로 업데이트 되어야 한다. $\Sigma_{t}$의 경우도 마찬가지이다.
\[\mu_{x_t \vert z_t} = \hat{\mu}_t + \hat{\Sigma}_t C^T (C \hat{\Sigma}_t C^T + R)^{-1} (z_t - C \hat{\mu}_t)\] \[\Sigma_{x_t \vert z_t} = \hat{\Sigma}_t - \hat{\Sigma}_t C^T (C \hat{\Sigma}_t C^T + R)^{-1} C \hat{\Sigma}_t\]위 식에서 Kalman Gain $K_t$를 다음과 같이 정의할 수 있다.
\[K_t = \hat{\Sigma}_t C^T (C \hat{\Sigma}_t C^T + R)^{-1}\]Perfect Sensor ($R=0$)의 경우 $K_t = C^{-1}$, $\mu_t = C^{-1}z_t$, $\Sigma_t = 0$이 되고,
Horrible Sensor ($R \to \infty$)의 경우 다음과 같아지는 것을 볼 수 있다.
\[K_t = \hat{\Sigma}_t C^T (C \hat{\Sigma}_t C^T + R)^{-1} \to 0\] \[\mu_t = \hat{\mu}_t + K_t (z_t - C \hat{\mu}_t) \to \hat{\mu}_t\] \[\Sigma_t = \hat{\Sigma}_t - K_t C \hat{\Sigma}_t \to \hat{\Sigma}_t\]$K_t$로 간단히 나타내면 다음의 최종 결과를 얻는다.
\[\mu_t = \hat{\mu}_t + K_t (z_t - C \hat{\mu}_t)\] \[\Sigma_t = \hat{\Sigma}_t - K_t C \hat{\Sigma}_t\]IV. MATLAB 구현
Prediction Step:
function [covarEst,uEst] = pred_step(uPrev,covarPrev,ut,dt)
m = 0.5; k = 3.5; b = 2;
A = [0 1; -k/m -b/m];
B = [0; 1/m];
Q = [1; 1];
I = eye(2);
Ad = I + A*dt;
Bd = B*dt;
uEst = Ad*uPrev + Bd*ut;
covarEst = Ad*covarPrev*transpose(Ad) + Q*dt;
end
Update Step:
function [uCurr,covarCurr] = upd_step(z_t,covarEst,uEst)
C = [1 0];
Rp = 1;
K = covarEst*transpose(C)*inv(C*covarEst*transpose(C)+Rp);
uCurr = uEst + K*(z_t - C*uEst);
covarCurr = covarEst - K*C*covarEst;
end
Kalman Filter:
clear all; % Clear variables
close all;
clc;
datasetNum = 1; % 1 or 2
[Sampled_gt, MeasuredData, Impulse, sampledTime] = init(datasetNum);
% Measuring position
Z = MeasuredData(1,:); %all the measurements that you need for the update
% Set initial condition
uPrev = vertcat(Sampled_gt(:,1)); % Copy the true Initial state
covarPrev = eye(2); % Covariance constant
savedStates = zeros(2, length(sampledTime));
prevTime = 0; %previous time step in real time
for i = 1:length(sampledTime)
%Getting acceleration and input force for prediction step
ut = Impulse(i);
dt= sampledTime(i)-prevTime;
prevTime = sampledTime(i);
z_t=Z(i);
%Getting Prediction Step
[covarEst,uEst] = pred_step(uPrev,covarPrev,ut,dt);
%Getting Updated Step
[uCurr,covar_curr] = upd_step(z_t,covarEst,uEst);
%Saving the new State
savedStates(:,i) = uCurr;
%updating for next iteration
uPrev = uCurr;
covarPrev = covar_curr;
end
plotData(savedStates, sampledTime, Sampled_gt, 1, datasetNum);
이런 식으로 짜고 DataSet만 적절히 넣어주면 된다.
Results
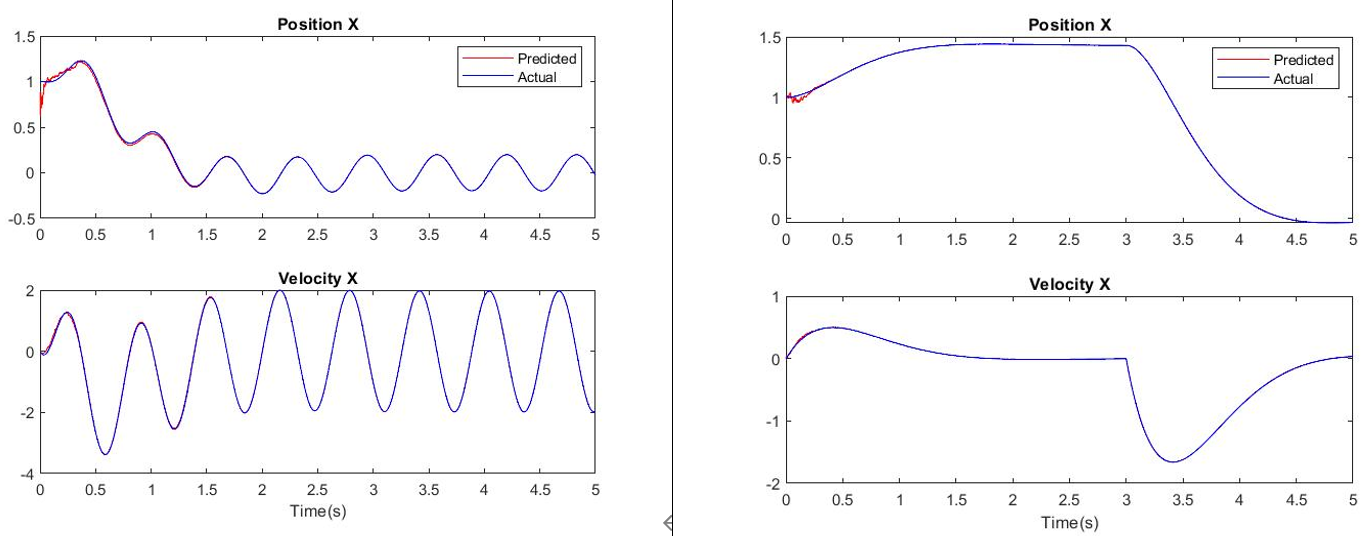
관측 값을 이용해서 예측한 경로와 실제 경로가 거의 일치하는 것을 볼 수 있다.
뉴욕대학교 Giuseppe Loianno 교수님의 ROB-UY3303 Robot Motion and Planning 강의 자료를 기반으로 작성되었음
2024/09/18