Variational Autoencoders
1. Latent Variable Models
Latent variable models는 $Pr(\mathbf{x})$ 대신에 latent variable $\mathbf{z}$를 이용하여 $Pr(\mathbf{x}, \mathbf{z})$ 를 표현함으로써 $Pr(\mathbf{x})$ 를 간접적으로 나타낸다.
\[Pr(\mathbf{x}) = \int Pr(\mathbf{x} ,\mathbf{z})d\mathbf{z}\]Conditional probability로 풀어서 작성하면 아래 식처럼 된다.
\[Pr(\mathbf{x}) = \int Pr(\mathbf{x} \vert \mathbf{z})Pr(\mathbf{z})d\mathbf{z}\]$Pr(\mathbf{x})$가 복잡하면 $Pr(\mathbf{x} \vert \mathbf{z})$ 와 $Pr(\mathbf{z})$ 로 간접적으로 나타내는 것이 상대적으로 간단할 수 있다.
Mixture of Gaussians
\[Pr(z = n) = \lambda _n\] \[Pr(x \vert z = n) = N_x \left[\mu _n, {\sigma _n}^2\right]\]잠재변수 $z$는 discrete 하게 주어지는 값이므로 가능한 값들을 모두 더해서 marginalize 할 수 있다. 주어진 $z$ 값에 따라 $x$의 분포는 평균이 $\mu _n$이고 분산이 $(\sigma _n)^2$인 정규분포를 따른다.
\[Pr(x) = \sum\limits_{i=1}^N Pr(x, z=n)\] \[= \sum\limits_{i=1}^N Pr(x \vert z=n) \cdot Pr(z=n) = \sum\limits_{i=1}^N \lambda_n \cdot N_x \left[\mu _n, {\sigma _n}^2\right]\]이를 통해 복잡한 multi-modal 확률 분포를 간단한 likelihood와 prior로 나타낼 수 있다.
2. Nonlinear Latent Variable Model
Nonlinear latent variable model에서는 data $\mathbf{x}$ 와 latent variable $\mathbf{z}$ 모두 continuous 이고 multivariate이다.
\[Pr(\mathbf{z}) = N_\mathbf{z}\left[\mathbf{0}, \mathbf{I}\right]\]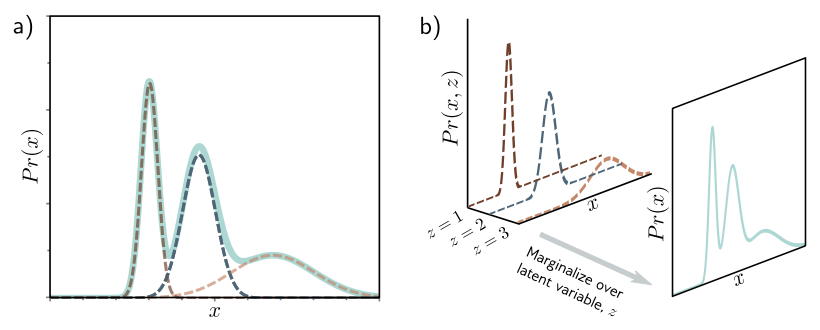
복잡한 분포를 여러 가우시안의 Weighted Sum으로 설명할 수 있으므로, discrete latent variable $z$ 를 도입하여 하나의 가우시안 분포인 Joint Probability $Pr(\mathbf{x}, \mathbf{z})$를 Marginalize 함으로써 $Pr(x)$를 구하는 것이다.
\[Pr(\mathbf{x} \vert \mathbf{z}, \boldsymbol{\phi}) = N_\mathbf{x} \left[\mathbf{f}\left[\mathbf{z}, \boldsymbol{\phi}\right], \sigma^2 \mathbf{I}\right]\]$\mathbf{f}\left[\mathbf{z}, \boldsymbol{\phi}\right]$ 은 deep network parameter $\boldsymbol{\phi}$ 로 표현되고, 데이터의 중요한 특징을 설명한다. 나머지 설명되지 않는 부분들은 노이즈 $\sigma^2 \mathbf{I}$에 포함된다.
잠재 변수 $\mathbf{z}$ 에 대해 marginalizing 하면 $Pr(\mathbf{x} \vert \boldsymbol{\phi})$ 를 얻을 수 있다.
\[Pr(\mathbf{x} \vert \boldsymbol{\phi}) = \int Pr(\mathbf{x} \vert \mathbf{z}, \boldsymbol{\phi}) \cdot Pr(\mathbf{z}) d\mathbf{z} = \int N_\mathbf{x} \left[\mathbf{f}\left[\mathbf{z}, \boldsymbol{\phi}\right], \sigma^2\mathbf{I}\right] \cdot N_\mathbf{z} \left[\mathbf{0}, \mathbf{I}\right] d\mathbf{z}\]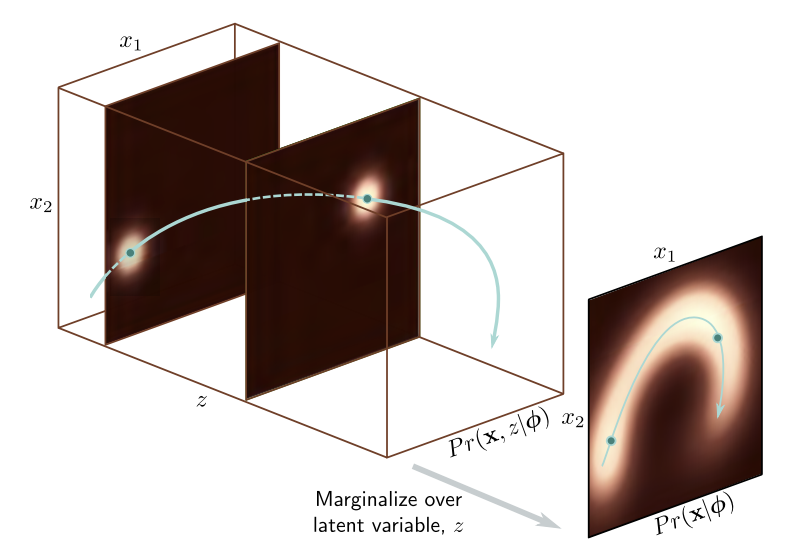
Generation
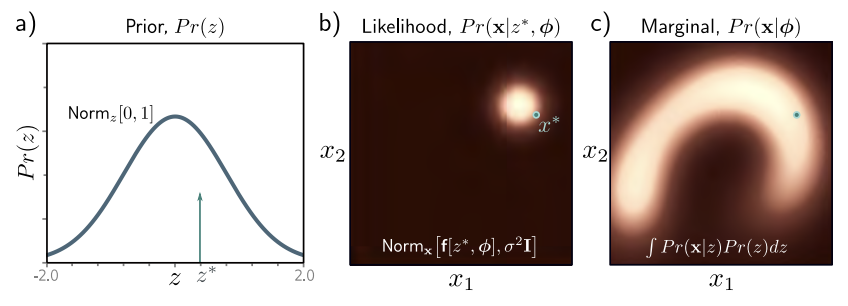
$Pr(z)$로부터 $z^{\ast}$ 추출하고 $\mathbf{f}\left[z^{\ast}, \boldsymbol{\phi}\right]$에 통과시켜 $Pr(\mathbf{x} \vert z^{\ast}, \boldsymbol{\phi})$의 mean을 구한다. Variance는 $\sigma^2 \mathbf{I}$로 고정된 값이다. 이것으로부터 $\mathbf{x}^{\ast}$를 추출한다. 이 과정을 반복하면 $Pr(\mathbf{x} \vert \boldsymbol{\phi})$를 얻을 수 있다. 이처럼 Ancestral sampling으로 sample $\mathbf{x}^{\ast}$을 생성한다.
3. Training
모델을 학습시키려면 log-likelihood를 maximize 하는 $\boldsymbol{\phi}$을 찾아야 하지만, 이것은 intractable 하기 때문에 ELBO를 이용한다.
\[\hat{\boldsymbol{\phi}} = \argmax_\phi \left[\sum\limits_{i=1}^I log\left[Pr(\mathbf{x}_i \vert \boldsymbol{\phi})\right]\right]\]where:
\[Pr(\mathbf{x}_i \vert \boldsymbol{\phi}) = \int N_\mathbf{x} \left[\mathbf{f}\left[\mathbf{z}, \boldsymbol{\phi}\right], \sigma^2\mathbf{I}\right] \cdot N_\mathbf{z} \left[\mathbf{0}, \mathbf{I}\right] d\mathbf{z}\]Evidence Lower Bound (ELBO)
ELBO는 주어진 log-likelihood 보다 항상 같거나 작은 함수이다. ELBO를 최대화 하여 원래 log-likelihood를 간접적으로 최대화 하는 $\boldsymbol{\phi}$를 찾는 것이다. ELBO는 다른 파라미터 $\boldsymbol{\theta}$ 에 의존할 수 있다. ELBO를 정의할 때 Jensen’s inequality가 필요하다.
Jensen’s Inequality
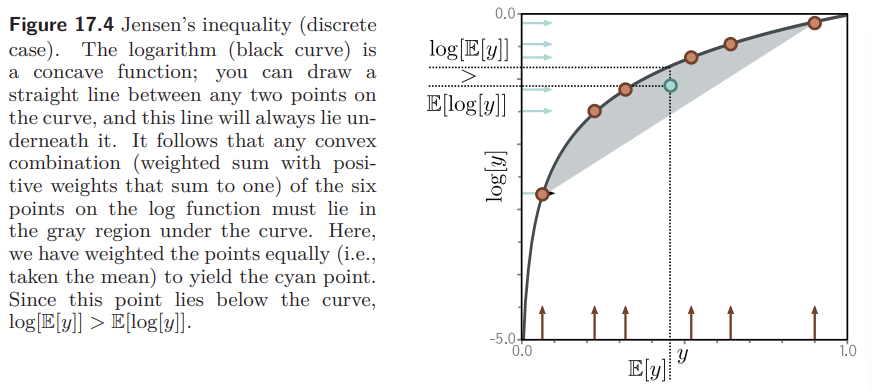
Concave Function에 대해 데이터의 기댓값이 항상 데이터의 함숫값의 기댓값보다 같거나 크다는 것이다.
1) discrete case
2) continuous case
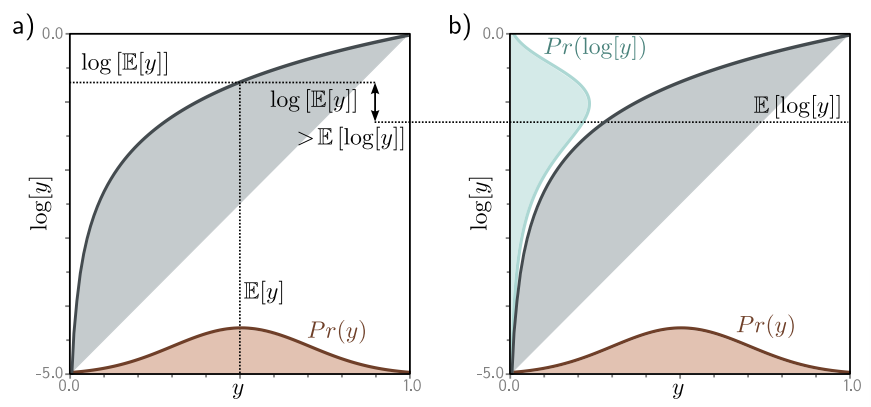
Concave Function이면 어떤 점들을 이어도 함수보다 밑에 위치하게 된다. 로그 함수는 concave function이므로 다음 식이 항상 성립할 것을 알 수 있다.
\[log\left[E\left[y\right]\right] > E\left[log\left[y\right]\right]\] \[log\left[\int Pr(y)ydy\right] \geq \int Pr(y)log\left[y\right]dy\]Pr(y)에 대한 제한이 없으므로, y에 대한 새로운 확률 분포를 나타내는 random variable $h\left[y\right]$에 대해서도 성립한다.
\[log\left[\int Pr(y)h\left[y\right]dy\right] \geq \int Pr(y)log\left[h\left[y\right]\right]dy\]Deriving the bound
이제 Log-likelihood의 lower bound를 유도하기 위해 Jensen’s inequality를 이용한다. 먼저 잠재변수 $\mathbf{z}$에 대한 임의의 확률 분포인 $q(\mathbf{z})$를 도입한다.
\[log\left[Pr(\mathbf{x} \vert \boldsymbol{\phi})\right] = log\left[\int Pr(\mathbf{x, z} \vert \boldsymbol{\phi})d\mathbf{z}\right] = log\left[\int q(\mathbf{z})\frac{Pr(\mathbf{x, z} \vert \boldsymbol{\phi})}{q(\mathbf{z})}\right]d\mathbf{z}\]위의 Jensen’s inequality 식에서 $Pr(y)$가 $q(\mathbf{z})$에 해당하고 나머지가 $h\left[y\right]$ 라고 보면 이해가 쉽다.
\[log\left[\int q(\mathbf{z})\frac{Pr(\mathbf{x, z} \vert \boldsymbol{\phi})}{q(\mathbf{z})}d\mathbf{z}\right] \geq \int q(\mathbf{z}) log\left[\frac{Pr(\mathbf{x, z} \vert \boldsymbol{\phi})}{q(\mathbf{z})}\right]d\mathbf{z}\]이 부등식에서 오른쪽 부분이 ELBO라고 보면 된다. $q(\mathbf{z})$가 $\boldsymbol{\theta}$ 를 파라미터로 가지므로 ELBO는 다음과 같다. $\boldsymbol{\theta}$는 뒤에서 ($\boldsymbol{\mu}$, $\boldsymbol{\Sigma}$)라고 보면 될 것 같다.
\[ELBO\left[\boldsymbol{\theta}, \boldsymbol{\phi}\right] = \int q(\mathbf{z} \vert \boldsymbol{\theta}) log\left[\frac{Pr(\mathbf{x, z} \vert \boldsymbol{\phi})}{q(\mathbf{z} \vert \boldsymbol{\theta})}\right]d\mathbf{z}\]4. ELBO properties
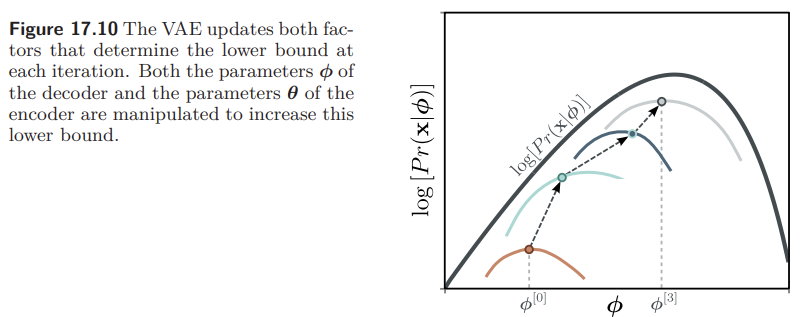
$log\left[Pr(\mathbf{x} \vert \boldsymbol{\phi})\right]$ 는 $\boldsymbol{\phi}$ 의 함수이므로 x축에 해당하는 $\boldsymbol{\phi}$ 에 대해서만 값이 변한다. 반면 ELBO는 $\boldsymbol{\phi}$ 와 $\boldsymbol{\theta}$ 의 함수이므로, 두 파라미터를 조정하면서 최적의 ELBO 값을 찾아야 한다. $\boldsymbol{\theta}$ 를 조정하면 ELBO 함수 자체가 바뀌게 되고, $\boldsymbol{\phi}$ 를 조정하면 ELBO 함수는 그대로인 상태에서 그 함수를 따라 움직이게 된다.
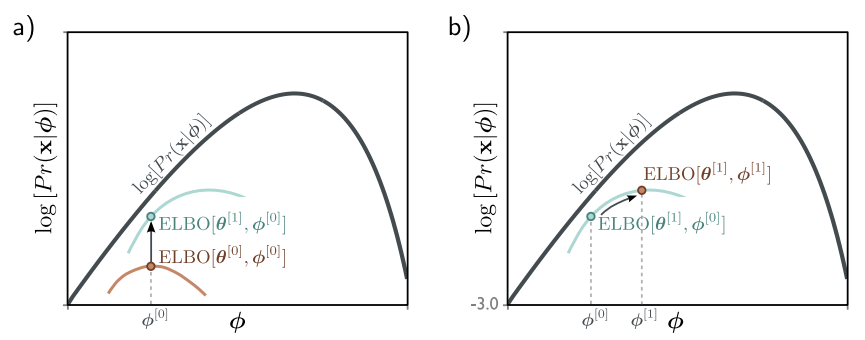
Tightness of bound
고정된 $\phi$ 에 대해서 ELBO와 likelihood function이 닿으면 ELBO가 tight 하다고 표현한다. ELBO를 tight 하게 하는 $q(\mathbf{z} \vert \boldsymbol{\theta})$ 를 찾기 위해 조건부 확률을 이용한다. 4번째 줄에서는 $\int q(\mathbf{z} \vert \boldsymbol{\theta}) d\mathbf{z} = 1$ 이고, $log\left[Pr(\mathbf{x} \vert \boldsymbol{\phi})\right]$ 는 z와 independent 하다는 점이 사용되었다.
\[ELBO\left[\boldsymbol{\theta}, \boldsymbol{\phi}\right] = \int q(\mathbf{z} \vert \boldsymbol{\theta}) log\left[\frac{Pr(\mathbf{x, z} \vert \boldsymbol{\phi})}{q(\mathbf{z} \vert \boldsymbol{\theta})}\right]d\mathbf{z}\] \[= \int q(\mathbf{z} \vert \boldsymbol{\theta}) log\left[\frac{Pr(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\phi})Pr(\mathbf{x} \vert \boldsymbol{\phi})}{q(\mathbf{z} \vert \boldsymbol{\theta})}\right]d\mathbf{z}\] \[= \int q(\mathbf{z} \vert \boldsymbol{\theta}) log\left[Pr(\mathbf{x} \vert \boldsymbol{\phi})\right] d\mathbf{z} + \int q(\mathbf{z} \vert \boldsymbol{\theta}) log \left[\frac{Pr(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\phi})}{q(\mathbf{z} \vert \boldsymbol{\theta})}\right]d\mathbf{z}\] \[= log\left[Pr(\mathbf{x} \vert \boldsymbol{\phi})\right] + \int q(\mathbf{z} \vert \boldsymbol{\theta}) log \left[\frac{Pr(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\phi})}{q(\mathbf{z} \vert \boldsymbol{\theta})}\right]d\mathbf{z}\] \[= log\left[Pr(\mathbf{x} \vert \boldsymbol{\phi})\right] - D_{KL}\left[q(\mathbf{z} \vert \boldsymbol{\theta}) \vert \vert Pr(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\phi})\right]\]KL Divergence는 두 분포 간의 “distance”를 측정하며 non-negative 한 값을 갖는다. $q(\mathbf{z} \vert \boldsymbol{\theta}) = Pr(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\phi})$ 일 때 KL distance가 0이 되고 ELBO가 tight 해진다.
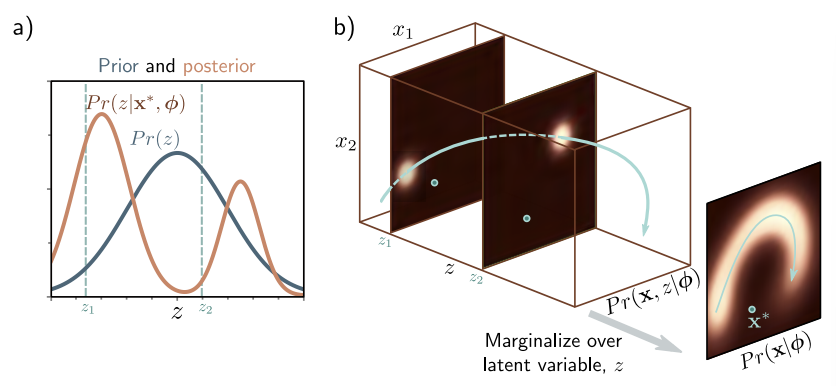
$Pr(z \vert \mathbf{x}^{\ast}, \boldsymbol{\phi})$ 은 관측된 데이터 $\mathbf{x}^{\ast}$ 를 만드는데 기여한 잠재 변수 $z$의 분포이다.
Posterior 분포인 $Pr(z \vert \mathbf{x}^{\ast}, \boldsymbol{\phi})$ 은 다음의 Bayes’ rule을 통해 계산된다.
\[Pr(z \vert \mathbf{x}^{\ast}, \boldsymbol{\phi}) \propto Pr(\mathbf{x}^{\ast} \vert z, \boldsymbol{\phi})Pr(z)\]ELBO as reconstruction loss minus KL distance to prior
ELBO 표현하는 또 다른 방법이다.
\[ELBO\left[\boldsymbol{\theta}, \boldsymbol{\phi}\right] = \int q(\mathbf{z} \vert \boldsymbol{\theta}) log\left[\frac{Pr(\mathbf{x, z} \vert \boldsymbol{\phi})}{q(\mathbf{z} \vert \boldsymbol{\theta})}\right]d\mathbf{z}\] \[= \int q(\mathbf{z} \vert \boldsymbol{\theta}) log\left[\frac{Pr(\mathbf{x} \vert \mathbf{z}, \boldsymbol{\phi})Pr(\mathbf{z})}{q(\mathbf{z} \vert \boldsymbol{\theta})}\right]d\mathbf{z}\] \[= \int q(\mathbf{z} \vert \boldsymbol{\theta}) log\left[Pr(\mathbf{x} \vert \mathbf{z}, \boldsymbol{\phi})\right] d\mathbf{z} + \int q(\mathbf{z} \vert \boldsymbol{\theta})log\left[\frac{Pr(\mathbf{z})}{q(\mathbf{z} \vert \boldsymbol{\theta})}\right] d\mathbf{z}\] \[= \int q(\mathbf{z} \vert \boldsymbol{\theta}) log\left[Pr(\mathbf{x} \vert \mathbf{z}, \boldsymbol{\phi})\right] d\mathbf{z} - D_{KL} \left[q(\mathbf{z} \vert \boldsymbol{\theta}) \vert\vert Pr(\mathbf{z})\right]\]첫번째 항은 잠재 변수와 데이터 간의 average agreement를 측정한다. 잠재변수 $\mathbf{z}$ 를 통해 원래 분포를 여러 개의 단일 가우시안의 합으로 표현하는데, 이때 얼마나 잘 들어맞는지를 나타내는 항으로 보면 된다. 이 항은 reconstruction loss라고 불린다. 두번째 항은 $Pr(\mathbf{z})$ 와 $q(\mathbf{z} \vert \boldsymbol{\theta})$ 가 얼마나 비슷한지를 나타내며 VAE에 이용되는 공식 중에 하나이다.
5. Variational Approximation
위에서 $q(\mathbf{z} \vert \boldsymbol{\theta}) = Pr(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\phi})$ 일 때 ELBO가 tight 하다는 점을 유도했다. Bayes’ rule을 적용하면 Posterior $Pr(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\phi})$ 를 다음과 같이 계산할 수 있다.
\[Pr(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\phi}) = \frac{Pr(\mathbf{x} \vert \mathbf{z}, \boldsymbol{\phi})Pr(\mathbf{z})}{Pr(\mathbf{x} \vert \boldsymbol{\phi})}\]그러나 실제로는 $Pr(\mathbf{x} \vert \boldsymbol{\phi})$ 를 계산할 수 없으므로 $Pr(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\phi})$ 는 intractable하다.
따라서 $q(\mathbf{z} \vert \boldsymbol{\theta})$ 가 $Pr(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\phi})$ 에 가장 가까워지도록 근사를 하게 된다.
\[q(\mathbf{z} \vert \boldsymbol{\theta}) \approx Pr(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\phi})\]$Pr(\mathbf{z} \vert \mathbf{x})$ 와 가장 가까운 multivariate normal gaussian을 찾는 것이다. 두번째 ELBO 식에서 $D_{KL}$을 줄이는 것과 같다.
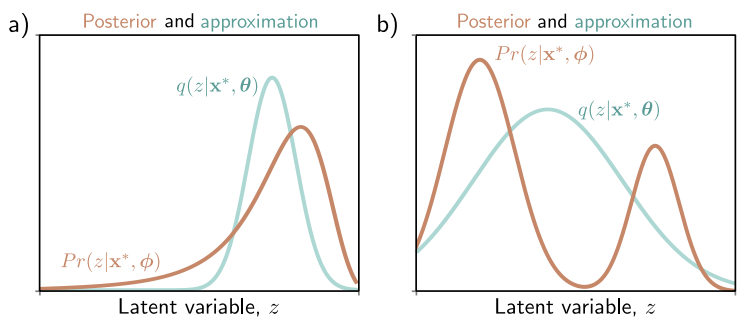
$q(\mathbf{z} \vert \boldsymbol{\theta})$ 의 optimal choice가 posterior $Pr(\mathbf{z} \vert \mathbf{x})$ 인데, posterior이 $\mathbf{x}$ 에 의존하므로 q를 다음과 같이 선택할 수 있다.
\[q(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\theta}) = N_{\mathbf{z}} \left[\boldsymbol{g_{\mu}}\left[\mathbf{x}, \boldsymbol{\theta}\right], \boldsymbol{g_{\Sigma}}\left[\mathbf{x}, \boldsymbol{\theta}\right]\right]\]$\boldsymbol{g}\left[\mathbf{x}, \boldsymbol{\theta}\right]$ 는 parameter $\boldsymbol{\theta}$를 가지며, mean $\boldsymbol{\mu}$와 variance $\boldsymbol{\Sigma}$ 를 예측하는 second neural network이다.
6. The Variational Autoencoder
드디어 VAE를 표현할 수 있게 되었다.
\[ELBO\left[\boldsymbol{\theta}, \boldsymbol{\phi}\right] = \int q(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\theta}) log\left[Pr(\mathbf{x} \vert \mathbf{z}, \boldsymbol{\phi})\right] d\mathbf{z} - D_{KL}\left[q(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\theta}) \vert\vert Pr(\mathbf{z})\right]\]첫번째 항은 여전히 intractable 하지만, 기댓값을 구하는 것이기 때문에 Monte Carlo Estimate으로 근사하여 구할 수 있다.
\[E_{\mathbf{z}}\left[a\left[\mathbf{z}\right]\right] = \int a\left[\mathbf{z}\right]q(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\theta}) d\mathbf{z} \approx \frac{1}{N} \sum \limits_{n=1}^{N} a\left[\mathbf{z}_n^{\ast}\right]\]n개의 sample의 기댓값을 구해서 전체의 기댓값으로 근사하는 것이다.
근사를 많이 하게 되면, 하나의 $\mathbf{z}^{\ast}$ 만 이용할 수도 있다. (n=1인 경우)
\[ELBO\left[\boldsymbol{\theta}, \boldsymbol{\phi}\right] \approx \int q(\mathbf{z}^{\ast} \vert \mathbf{x}, \boldsymbol{\theta}) log\left[Pr(\mathbf{x} \vert \mathbf{z}, \boldsymbol{\phi})\right] d\mathbf{z} - D_{KL} \left[q(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\theta}) \vert\vert Pr(\mathbf{z})\right]\]두번째 항은 $q(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\theta}) = N_{\mathbf{z}}\left[\boldsymbol{\mu}, \boldsymbol{\Sigma}\right]$ 와 $Pr(\mathbf{z})=N_{\mu}\left[\mathbf{0}, \mathbf{I}\right]$ 간의 KL divergence이다. 두 정규분포의 KL divergence는 다음과 같이 계산될 수 있다.
\[D_{KL}\left[q(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\theta}) \vert\vert Pr(\mathbf{z})\right] = \frac{1}{2} (Tr\left[\boldsymbol{\Sigma}\right] + \boldsymbol{\mu}^{T}\boldsymbol{\mu} - D_{\mathbf{z}} - log\left[det\left[\boldsymbol{\Sigma}\right]\right])\]$D_{\mathbf{z}}$ 는 latent space의 dimensionality이다.
VAE algorithm
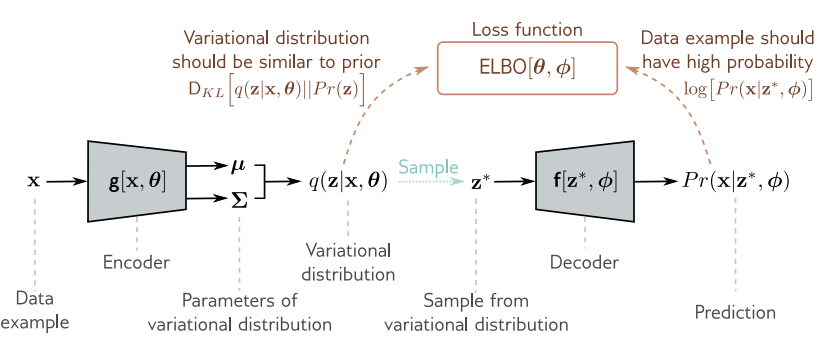
인코더 $\mathbf{g}\left[\mathbf{x}, \boldsymbol{\theta}\right]$ 는 training example인 $\mathbf{x}$를 인풋으로 받은 후 Variational distribution $q(\mathbf{z} \vert \mathbf{x}, \boldsymbol{\theta})$ 의 parameter인 $\boldsymbol{\mu}$ 와 $\boldsymbol{\Sigma}$ 를 찾는다. 이 분포로부터 $\mathbf{z}^{\ast}$ 를 샘플링 하고 이것을 디코더 $\mathbf{f}\left[\mathbf{z}, \boldsymbol{\phi}\right]$ 에 넣어서 데이터 $\mathbf{x}$ 를 예측한다. Loss function은 negative ELBO이다.
ELBO를 계산할 때 $\boldsymbol{\phi}$ 와 $\boldsymbol{\theta}$ 를 모두 변화시킨다. 또한 SGD나 Adam과 같은 optimizer를 이용한다.
The reparameterization trick
앞의 네트워크는 sampling step을 포함하므로 미분하기가 아주 어렵다. 하지만 $\boldsymbol{\theta}$ 를 업데이트 하기 위해서는 미분 과정이 필수적이다.
간단한 솔루션은 이러한 stochastic part는 네트워크의 branch로 빼내는 것이다. 이렇게 되면 backpropagation 시에 sampling step을 거칠 필요가 없다.
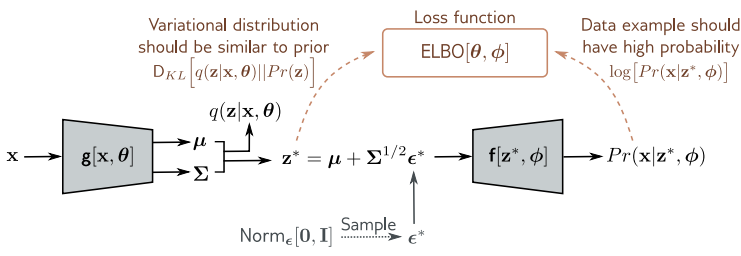
표준 정규 분포에서 $\boldsymbol{\epsilon}^{\ast}$ 을 sampling 한 뒤 이것을 통해서 $\mathbf{z}^{\ast}$ 를 구한다.
\[\mathbf{z}^{\ast} = \boldsymbol{\mu} + \boldsymbol{\Sigma}^{1/2}\boldsymbol{\epsilon}^{\ast}\]Reference
Understanding Deep Learning (Simon J.D. Prince, The MIT Press, 2023)
2024/08/18